Buoyancy

The buoyancy of an object for example a ship hull can be determined using Archimedes' principle. Archimedes' principle states that: "Any object, totally or partially immersed in a fluid or liquid, is buoyed up by a force equal to the weight of the fluid displaced by the object."

The forces acting on a fully or partly immersed object can be calculated as the force will depend on the gravitational acceleration, the volume of the immersed part of the object and the density of the liquid.

Buoyant upward force:

\begin{align} F_b=\rho gV \end{align}

where:

g - the gravitational acceleration \( 9.81m/s^2 \)
V - the volume of the immersed part of the object
ρ - density of the liquid

The other force acting on the body is the downward force due to the mass of the object

\begin{align} F_w=mg \end{align}

where:

g - the gravitational acceleration \( 9.81m/s^2 \)
m - mass of the object

The resulting force or net force F_r is the difference between the two forces. It will equal zero when the immersed object is at equilibrium.

\begin{align} F_r = F_w-F_b = mg-\rho gV=0 \end{align}

From this it can be derived that the mass of the object is equal to the mass for the displaced liquid.

\begin{align} mg-\rho gV& =0 \\ m& = \rho V \end{align}

Pressure

Another way to determine the bouyant force is to look at the pressures affecting the immersed object. Hydrostatic pressure is as described in this article a function of liquid density, the gravitational acceleration and the depth below the liquid surface.

\begin{align} p=\rho gh \end{align}

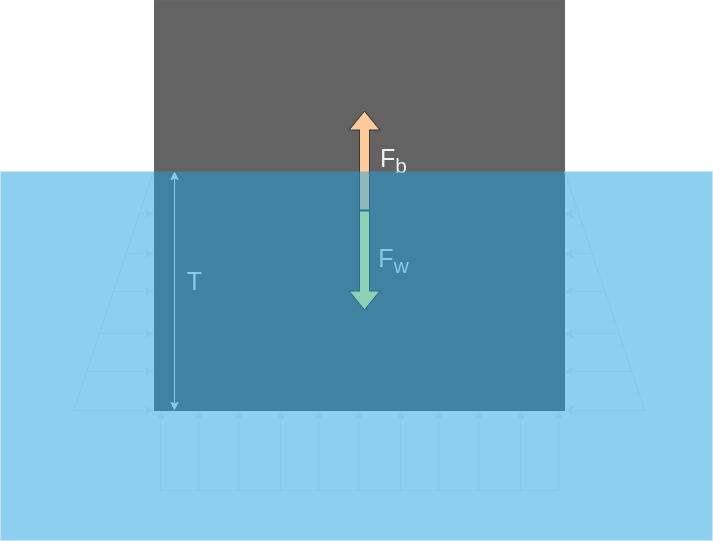
The sketch below illustrates the pressure acting on a immersed object. The pressure on the side varies linearly with the depth below the surface and the pressures on the sides will cancel each other out. If not we would have invented a device that could move without using any fuel. The pressure on the bottom is constant as the bottom is completely flat and is at a constant depth.

The buyant force is calculated

\begin{align} F_b=p\cdot A= \rho g TLB \end{align}

where

p is the pressure acting on the bottom
A is the area of the bottom \( A=LB \)
ρ is the density of the
T is the draught of the object or vertical distance from bottom the liquid surface
L is the length of the object
B is the breadth of the object

Ones again we will look at the resulting force and setting it equal to zero when the immersed object is at rest.

\begin{align} F_r = F_w-F_b = mg-\rho g TLB=0 \end{align}

The mass of the object can ones again be determined.

\begin{align} m = \rho TLB = \rho V \end{align}

As seen the mass is as shown again only a function of liquid density and displaced volume when realizing that the displaced volume is equal to \( V=TLB \)

Illustration of forces and pressures acting on a floating object

Submarine example

The biggest ever built submarine is the Russian Typhoon class. It displaces 48000t when submerged.

It is in this example fully submerged with only the upper part of the periscope above the water surface and with no movement.

What happens when an Albatross lands gently on the periscope? The weight of the albatross is 10kg which is next to nothing when compared to the displacement of the submarine 48000t or 48000000kg.

The diameter of the periscope is estimated to 20cm and the liquid is sea water with a density of 1025kg/m³.

First step is to calculate how much additional water has to be displaced after the albatross has landed.

\begin{align} V = \frac{m}{\rho } = \frac{10kg}{1025kg/m^3 }=9.76\cdot 10^{-3}m^3 = 9.76L \end{align}

Only the periscope can add additional displaced volume to carry the albatross as the rest of the submarine is already submerged.

The waterplane area or cross-sectional area of the periscope is:

\begin{align} A = \frac{\pi }{4}D^2 = \frac{\pi }{4}0.20m^2=3.14\cdot 10^{-2}m^2 \end{align}

The additional draught of the submarine after the albatross has landed

\begin{align} T_{additional}=\frac{V}{A}=\frac{9.76\cdot 10^{-3}m^3}{3.14\cdot 10^{-2}m^2}=0.31m=31cm \end{align}

As seen the submarine draught will increase 31cm when the albatross has landed eventhough the weight of the albatross is very small compared to the weight of the submarine.